vBAddict » wot Statistik und Performance Analyzer
Für manche ist es das zwanglose Ballern, für andere hingegen ist es eine Frage der Strategie. Letztendlich liegt die Wahrheit in der Mitte, denn World of Tanks ist eine Taktik-Shooter Panzer Simulation. Wer einfach nur blind drauflos schießen möchte, wird meist keinen Erfolg haben. Und wer sich tatsächlich verbessern möchte, um auf dem Schlachtfeld wirklichen Fortschritt zu haben, der muss die Sache sogar etwas ernsthafter angehen. Dazu sollte man seine eigenen Runden analysieren und vielleicht auch einen Blick auf die Runden anderer Spieler werfen. Mit vBAddict.net ist das möglich, denn hierbei handelt es sich um einen World of Tanks Analyzer. Perfekt für alle, die Statistiken lieben und sich auch für das beliebte MMO Game erfreuen können. Wie der wot stats Analyzer funktioniert, gibt es in den folgenden Absätzen zu erfahren.

vBAddict – Persönliche Statistiken zu World of Tanks
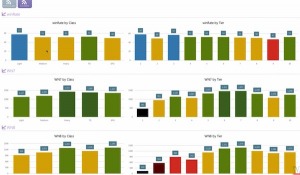
Vor allem ist dabei auch interessant, dass man sich mit anderen Spielern vergleichen kann. Das geht, weil eine Spielerwertung existiert, die als WN8 bezeichnet wird. Natürlich bietet vBAddict damit auch einen großen Anreiz, dass man sich immer weiter verbessert, um so seine Mitspieler zu übertrumpfen. Möglich machen das übrigens lokal gespeicherter Cache Dateien, die automatisch vom Spiel angelegt werden und hochgeladen werden können. In diesen Dateien finden sich allerhand Informationen über Runden und Spieler.
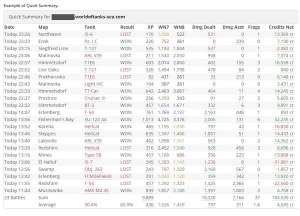
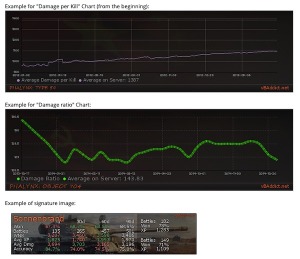
Interessant ist wirklich die Informationsdichte, die dabei hilft, dass man eine Runde noch einmal aus einer ganz anderen Perspektive wahrnehmen kann. Aufgelistet werden beispielsweise die Effizienz, die Zielgenauigkeit, der Schadenswert, der erhaltene Schaden und auch den Schaden, den man durch Assists ausgeteilt hat. Auch wie viel Schaden man pro Kill braucht, die Erfahrung, die durchschnittliche Zeit einer Runde oder die Entfernung, die man auf der Map zurücklegt. Insofern gibt es also viel zu entdecken.
Besonders hilfreich bei der persönlichen Analyse ist, dass man sogar einen Spielverlauf minutiös nachvollziehen kann. Dafür gibt es eine Minimap, auf der man seine Bewegung Stück für Stück verfolgen kann. Übrigens auch von anderen Spielern. Wer also wirklich bis ins Detail seine Runden analysieren möchte, um sich verbessern zu können, hat hiermit das richtige Tool zur Hand.
So funktioniert der WoT Analyzer
Die Daten können online eingesehen werden, wo auch der Vergleich mit anderen Spielern möglich ist. Allerdings müssen die Daten auch erst einmal eingelesen werden, was nicht automatisch durch das Spiel geschieht. Mit der Hilfe des Clienten „Active Dossier Uploader“ können aber die Dateien einer Runde hochgeladen werden, um so auf vBAddict analysiert zu werden.
Dieser ADU-Client kann kostenlos heruntergeladen werden. Wer das Projekt unterstützen möchte, kann das über Spenden machen oder auch über die Anzeigen auf der Seite.
Der Erfolg von World of Tanks
Vorstellen muss man World of Tanks oberflächlich wohl nicht mehr, denn wer sich mit Spielen auskennt, wird früher oder später auch mal etwas von World of Tanks gehört haben. Das Spiel ist ein MMO, also ein Multiplayer Spiel im Internet. Es erschien 2014 und wird von Wargaming.net entwickelt. Das Studio ist auch gleichzeitig Publisher. Heute ist World of Tanks auf verschiedenen Plattformen verfügbar. Darunter die Xbox One, der PC und PlayStation 4. Gespielt werden kann mit Maus und Tastatur oder auch Controller.
In der 3D gestalteten Welt treffen Spieler auf andere Spieler. Angesetzt ist WoT im Zweiten Weltkrieg, wenn es auch Panzermodelle gibt, die aus späteren Zeiten stammen. Im Wesentlichen steuert jeder Spieler auf einer Map einen Panzer und macht dann Jagd auf den Gegner. Dafür werden zwei Teams mit bis zu 15 Spieler gebildet. Die Panzer unterscheiden sich in vielen Merkmalen. Manche sind leicht und wendig, andere schwerfälliger, aber mit stärkerer Feuerkraft. Die Panzer sind Originalen nachempfunden. Außerdem werden sie Nationen zugeordnet.
Fazit zu den wot stats von vBaddict.net
Wer von World of Tanks gar nicht genug bekommen kann und sich viele Gedanken über seine Runden und Fähigkeiten macht, für den ist vBAddict wohl genau die richtige Adresse. Diese Seite ermöglicht es, ein eigenes Spielerprofil anzulegen, das nach und nach mit Daten gefüttert wird, sodass man seine World of Tanks Karriere in Daten festhalten kann. So kann man sich auch mit anderen Spieler dank einer Spielerwertung vergleichen. Noch interessanter sind die Rundenauswertungen, die durch den Active Dossier Uploader möglich werden. Damit können die Dateien der Runden hochgeladen werden, sodass sie bis ins kleinste Detail analysiert werden können. Für Taktiker und Strategen ein wirklich mächtiges Werkzeug.